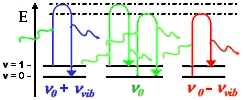
Обработка спектров в программном пакете Wolfram Mathematica
После непосредственного проведения КР эксперимента необходимо извлечь информацию из полученных данных не только качественно, но также и количественно. Для этого обычно применяются такие программные пакеты как PeakFit, Origin и другие. Один из них Wolfram Mathematica.
Преимущество этого программного пакета заключается в именно пакетной обработке данных, то есть в возможности обрабатывать последовательно, с помощью одного заданного начального условия, сразу большое количество файлов с данными эксперимента при разных внешних параметрах (температуре, давлении). Для удобства и точности подгонки, полученные подогнанные данные одного спектра одновременно являются начальными для следующего.
Для удобства и исключения каких либо неясностей при пакетной обработке спектров, в программе из имени файла считывается внешний параметр (температура, давление). Оно должно быть специфично - содержать в себе температуру в кельвинах, при которой был проведен данный эксперимент. Само имя файла следует разбить на несколько частей, например с помощью символа "_".
Пример текста программы, написанной в Wolfram Mathematica, для обработки данных КР :
При обработке спектров важную роль играет выбор модели для подгонки контуров. Ниже представлен фрагмент программы, где описывается одиннадцать функций подгонки, и два коэффициента Бозе – Эйнштейна (nbes, nbeas - для стоксовой и антистоксовой компоненты):
*При использовании в вычислениях физических констант нет необходимости вводить их численное значение. Достаточно в начале программы подключить пакет Physical Constants используя следующую запись:
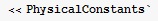
Самой распространенной и используемой во многих работах, ввиду универсальности, является модель Лоренца. Однако при описании низкочастотного диапазона спектра рекомендуется пользоваться функцией подгонки Harmonic (функция затухающего гармонического осциллятора). Кроме того, при работе с функцией Harmonic нет необходимости отдельно учитывать температурный фактор Бозе – Эйнштейна, ввиду того, что он является одним из составляющих этой функции. Ниже мы опишем два примера программы с использованием моделей для подгонки Harmonic и Lorentz:
1. Пример текста программы с использованием модели подгонки спектров Harmonic:
Полный текст программы:
Описание работы программы по шагам:
Задаем (MyPath) и выбираем(SetDirectory) директорию, в которой хранится папка с нужными нам файлами с экспериментальными данными
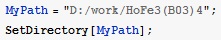
Выбираем тип и расширение файлов (*.txt)
Формируем форму вывода в файл
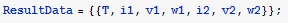
Здесь задаем модель для подгонки. Условие If присутствует вследствие того, что для функции Harmonic существует два варианта (для стоксовой и антистоксовой компоненты)
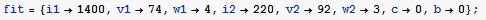
Задаем начальные данные для подгонки первого спектра
i1, v1,w1 – интенсивность, частота и ширина первой линии соответственно
i2, v2,w2 – интенсивность, частота и ширина второй линии соответственно
c, b – параметры базовой линии (наклон и уровень по оси Oy).
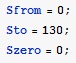
Значения Sfrom, Sto, Szero определяют
Sfrom и Sto – вырезают частотный интервал для подгонки (в данном случае это 0 – 130 cm-1)
Szero – значение на оси ординат, на котором закреплена ось абсцисс.
Далее следует цикл Do, перебирающий по одному файлу iName из указанной папки за один шаг. Выводится название файла
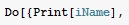……- начало цикла
- окончание цикла
В данном случае в цикле участвуют файлы с 1 по 100.
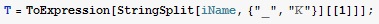
В этой строке происходит разбор имени файла на элементы (с помощью двух функций ToExpression и StringSplit) и считывание значения переменной T (температура, давление) из имени файла (iName). Стоит отметить, что имя файла должно быть специфично - содержать в себе температуру в кельвинах, при которой был проведен данный эксперимент. Само имя файла следует разбить на несколько частей, например с помощью символа "_".
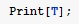
Вывод значения T.
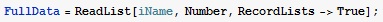
Считывание данных из выбранного файла с помощью функции ReadList и присвоение им имени FullData.
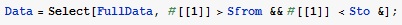
Выбираем нужный нам диапазон данных с помощью функции Select и присваиваем ему имя Data.
Функция FindFit является базовой функцией подгонки в Wolfram Mathematica. Максимальное число итераций – 5000.
*Здесь и далее символ /. означает подстановку значений, указанных после этого знака в выражение, стоящее до знака.
Вывод на экран исходных данных (Epilog-> Point [Data]) функцией Plot, полученных линий в отдельности (условие If[]), подогнанного спектра (model/.fit)
AxesOrigin – интервал значений по оси Ox
PlotRange – интервал значений по оси Oy
PlotStyle – совокупность параметров графика
Axes->True – видимость осей
Thickness – толщина линий
AxesLabel – подписи по осям.
Выделение подогнанных значений по точкам (функция Evaluate), соответственно данным из файла (iName).
Вычисляем разницу между подогнанными значениями и экспериментальными данными.
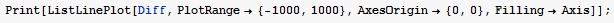
Вывод на экран значения Diff – погрешности подгонки (функция ListLinePlot)
PlotRange – интервал значений по оси Ox
AxesOrigin – точка пересечения осей
FillingAxis – заполнение цветом области под графиком.
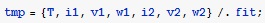
Присвоение массиву подогнанных значений имени tmp.
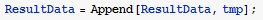
Дополнение массива ResultData массивом tmp на каждом шаге цикла (функция Append).
Вывод на экран массива значений tmp.
Окончание работы цикла.
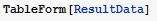
Вывод на экран полученных значений в табличной форме с помощью функции TableForm.
2. Пример текста программы с использованием модели подгонки спектров Lorentz:
Программа, описанная в данном параграфе, по своей структуре практически полностью соответствует программе, описанной ранее, за исключением модели подгонки.
Вследствие того, что при использовании модели подгонки Lorentz нужно отдельно учитывать температурный фактор Бозе - Эйнштейна, в тексте программы появился новый фрагмент.
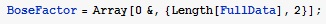
Задается массив чисел с именем BoseFactor. Он заполняется нулями, имеет два столбца и колличество строк такое же, как и у массива FullData.
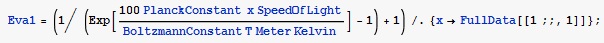
Задается массив элементов Eva1, который является фактором Бозе - Эйнштейна для стоксовой компоненты спектра (вычисляется для каждой точки массива FullData (массив экспериментальных данных)). Запись x-> FullData [[1; ;,1]] означает, что в выражении Eva1 переменная x принимает все значения первого столбца массива элементов FullData.
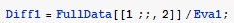
Вычисляется массив с именем Diff1с помощью массива Eva1 (фактора Бозе - Эйнштейна). Данная запись означает, что второй столбец массива FullData поэлементно делится на массив факторов Бозе - Эйнштейна.
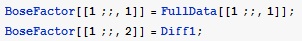
- присвоение значений каждому столбцу массива BoseFactor. первый столбец равенпервому стобцу массива экспериментальных данных Fulldata. Второму столбцу присваивается значение Diff1. Diff1 имеет смысл интенсивности в каждой точке экспериментального спектра, домноженную на обратный температурный фактор Бозе - Эйнштейна.
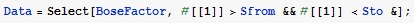- выбор интересующего нас спектрального диапазона с помощью функции Select. Аналогичная строка присутствует и в тексте программы, представленной в П.1, но исходным массивом там служит массив экспериментальных данных FullData.